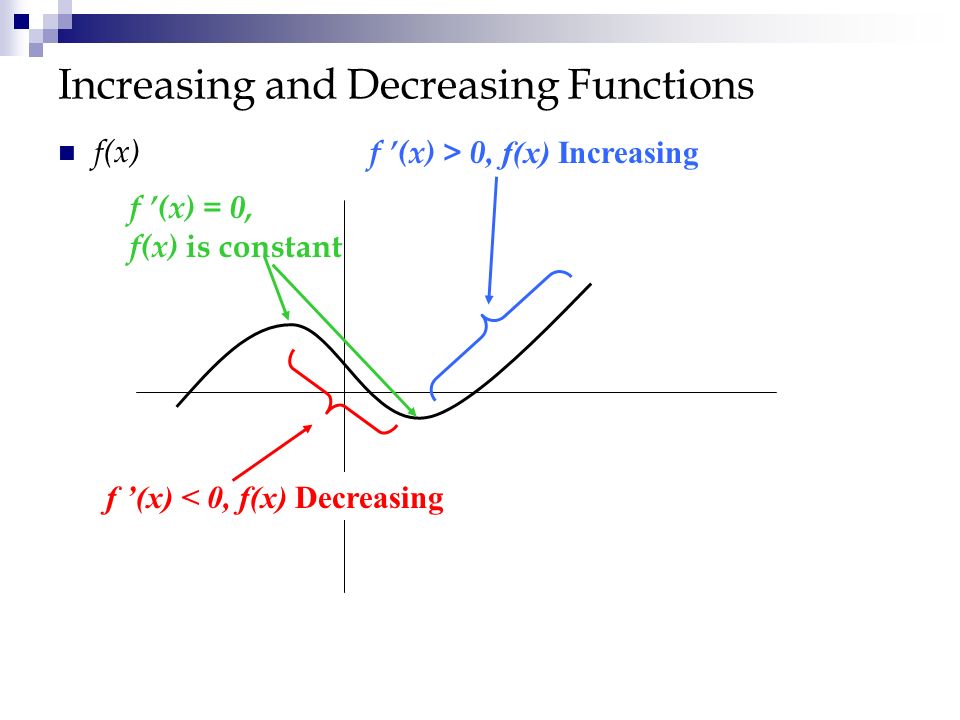
Use a graph of f(x) to determine the value of f(n), where n is a specific xvalueTable of Contents0000 Finding the value of f(2) from a graph of f(x)002Given the following graph, evaluate f(0) and solve for f(x) = 3 Solution To evaluate f(0) means to find the output of the function when the input is 0 To do this, find the point on the graph that has an xvalue of zero This will be the place where the graph crosses the yaxis For this function an input of 0 produces an output of 1On what interval is f decreasing?
Solving Polynomial Inequalities By Graphing
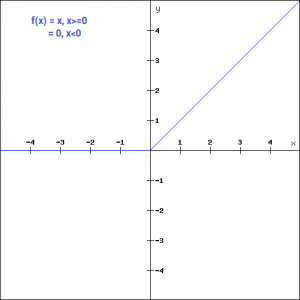
What is f(0) on a graph
What is f(0) on a graph- Transcript Ex 51, 8 Find all points of discontinuity of f, where f is defined by 𝑓(𝑥)={ (𝑥/𝑥, 𝑖𝑓 𝑥≠0@&0 , 𝑖𝑓 𝑥=0)┤ Since we need to find continuity at of the function We check continuity for different values of x When x = 0 When x > 0 When x < 0 Case 1 When x = 0 f(x) is continuous at 𝑥 =0 if LHL = RHL = 𝑓(0) Since there are two different Consider the graph of the function f(x)=x^2x12 a) Find the equation of the secant line joining the points (2,6) and (4,0) I got the equation of the secant line to be y=x4 b) Use the Mean Value Theorem to determine a point c




The Graph Of F X Is Given In The Figure Below Draw The Lines To The Graph At X 4 X 3 X 0 And X 3 Estimate F 4 F 3 F 0 And F 3 Study Com
The output f (x) is sometimes given an additional name y by y = f (x) The example that comes to mind is the square root function on your calculator The name of the function is \sqrt {\;\;} and we usually write the function as f (x) = \sqrt {x} On my calculator I input x for example by pressing 2 then 5 Then I invoke the function by pressingFrom the graph of f(x), draw a graph of f ' (x) We can see that f starts out with a positive slope (derivative), then has a slope (derivative) of zero, then has a negative slope (derivative) This means the derivative will start out positive, approach 0, and then become negative Be Careful Label your graphs f or f ' appropriatelyGraph f (x)=0 f (x) = 0 f ( x) = 0 Rewrite the function as an equation y = 0 y = 0 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the
Consider the function below f(x) = x1/x, x >B) Does f have a maximum or minimum value?0 (b) Explain the shape of the graph by computing the limit as x ?
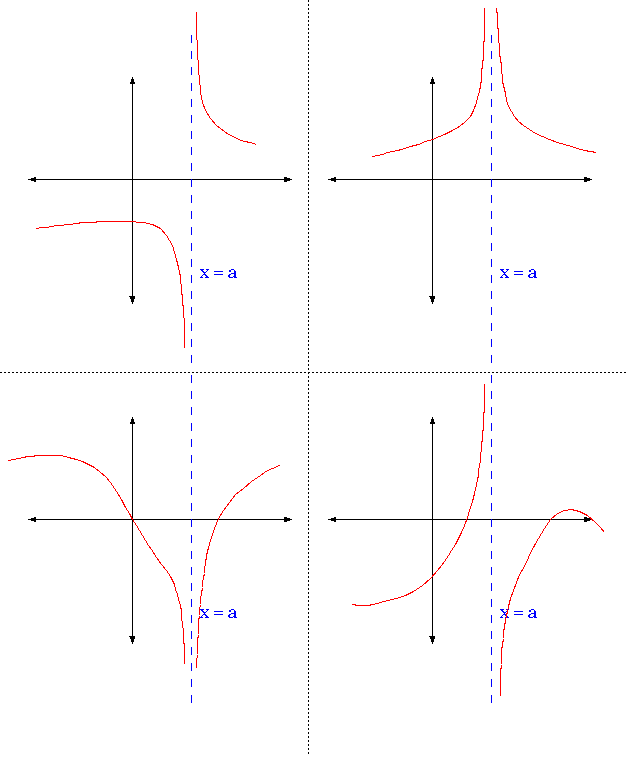
Translations of Functions Suppose that y = f(x) is a function and c > 0;Here is how this function looks on a graph with an xextent of 10, 10 and a yextent of 10, 10 First, notice the x and yaxes They are drawn in red The function, f (x) = 1 / x, is drawn in green Also, notice the slight flaw in graphing technology which is usually seen when drawing graphs of rational functions with computers or0 f(x) = lim x ?



On Line Math 21




Introduction To Limits In Calculus
0 and as x ?Use the given graph of y = f(x) to find the intervals on which f'(x) > 0, the intervals on which f'(x) < 0, and the values of x for which f'(x) = 0 Sketch a possible graph of y = f'(x) On what subinterval(s) is f'(x) > 0?Since f(0) = 1 ≥ 1 x2 1 = f(x) for all real numbers x, we say f has an absolute maximum over ( − ∞, ∞) at x = 0 The absolute maximum is f(0) = 1 It occurs at x = 0, as shown in Figure 412 (b) A function may have both an absolute maximum and an absolute minimum, just




Turning Points And Nature Iitutor



Graphs And The Derivative Chapter 13 Ch 13 Graphs And The Derivative 13 1 Increasing And Decreasing Functions 13 2 Relative Extrema 13 3 Higher Derivatives Ppt Download
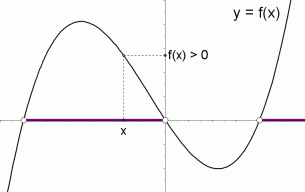
E) If f'(x)=0, then the x value is a point of inflection for f To illustrate these principles, consider the following problems 1) Suppose a) On what interval is f increasing?A quadratic function in the form f (x) = ax2 bxx f ( x) = a x 2 b x x is in standard form Regardless of the format, the graph of a quadratic function is a parabola The graph of y=x2−4x3 y = x 2 − 4 x 3 The graph of any quadratic equation is always a parabola Using the fact $f(x)>0$ on the interval where the graph is above the $x$axis, and $f(x)0$ for $x\in (3,2)\cup(0,2)\cup(3,\infty)$ b $f(x)



Web Viu Ca Pughg Summer12 Math121m12n01 Secondderivativenotes Pdf



Solution I Need Help With The Following Function Problem Find All Values Of X Such That F X Gt 0 And All X Such That F X Lt 0 And Sketch The Graph Of F F X Fourth Root Of
So we have the graphs of two functions here we have the graph y equals f of X and we have the graph y is equal to G of X and what I want to do in this video is evaluate what G of f of F let me do the F of in another color F of negative five is f of negative five is and it can sometimes see a little daunting when you see these composite functions you're taking you're evaluating the function GThe solution set of the equation 'f(x) =0 f (x) = 0 ' is shown in purple It is the set of all values of x x for which f(x) f (x) equals zero That is, it is the set of x x intercepts of the graph The graph of a function f f is shown at rightThe Function which squares a number and adds on a 3, can be written as f (x) = x2 5 The same notion may also be used to show how a function affects particular values Example f (4) = 4 2 5 =21, f (10) = (10) 2 5 = 105 or alternatively f x → x2 5 The phrase "y is a function of x" means that the value of y depends upon the value of




2 4 Function Compilations Piecewise Combinations And Composition Mathematics Libretexts




The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Brainly Com
A above 1 Example f (x) = (2)x For a above 1 As x increases, f (x) heads to infinity As x decreases, f (x) heads to 0 it is a Strictly Increasing function (and so is "Injective") It has a Horizontal Asymptote along the xaxis (y=0) Plot the graph here (use the "a" slider) •If the graph intersects or touches the Xaxis at EXACTLY ONE POINT then a quadratic polynomial has TWO EQUAL ZEROES (ONE ZERO)D= b² 4ac = 0 •If the graph is either completely above Xaxis or completely below Xaxis axis ie it DOES NOT INTERSECT XAXIS axis at any point Then the quadratic polynomial HAS NO ZERO D= b² 4ac < 0 Example 22 The function f is defined by 𝑓(𝑥)={ (1−&𝑥, 𝑥0)┤ Draw the graph of f (x) For x < 0 , f(x) = 1 – x We find the points to be plotted when x < 0 For x = 0 , f(x) = 1 Hence, point to be plotted is (0,1) For x > 0 , f(x) = x 1 We fi




Extrema Of A Function



Derivatives At Local Extrema Expii
The graph of y = f(x) c is obtained by translating the graph of y = f(x) c units upwards; Calculus AB Let f be the function that is given by f (x)= (axb)/ (x^2 c) It has the following properties 1) The graph of f is symmetrical with respect to the yaxis 2) The graph of f has a vertical asymptote at x=2 3) The graph of f passesConsider the function f ( x) = { 1 x if x ∈ ( 0, ∞) 0 else I know that this is the typical example of a discontinuous function whose graph is closed, but I can't see why it is closed I understand that I'm probably just being dumb here, but if x n → 0 , we have f ( x n) → ∞, so the graph



Curve Sketching F X



How Can You Tell The Difference Between A Function And Its Derivative On A Graph
Before we begin graphing, it is helpful to review the behavior of exponential growth Recall the table of values for a function of the form f (x) = b x f (x) = b x whose base is greater than one We'll use the function f (x) = 2 x f (x) = 2 x Observe how the output values in Table 1 change as the input increases by 1 1Graph f (x)=2x f (x) = 2x f ( x) = 2 x Rewrite the function as an equation y = 2x y = 2 x Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using Given the graph of a function f, we can construct the graph of its antiderivative F provided that (a) we know a starting value of F, say F(a), and (b) we can evaluate the integral ∫b af(x)dx exactly for relevant choices of a and b For instance, if we wish to know F(3), we can compute F(3) = F(a) ∫3 af(x)dx



Graphical Interpretation Of Sentences Like F X 0 And F X 0



Derivative And Tangent Line
The graph of an exponential function is a strictly increasing or decreasing curve that has a horizontal asymptote Let's find out what the graph of the basic exponential function y = a x y=a^x y = ax looks like (i) When a > 1, a>1, a > 1, the graph strictly increases as x HSBC244 has shown a nice graph that has derivative #f'(3)=0# Here are couple of graphs of functions that satisfy the requirements, but are not differentiable at #3# #f(x) = abs(x3)5# is shown below graph{y = abs(x3)5 14, 25, 616, 1185} #f(x) = (x3)^(2/3) 5# is shown on the next graphSee the answer Find all values of x such that f (x) > 0 and all x such that f (x) < 0 and sketch the graph of f 1) Answer f (x) > 0 if x < 2 or 0< x< 4 ;
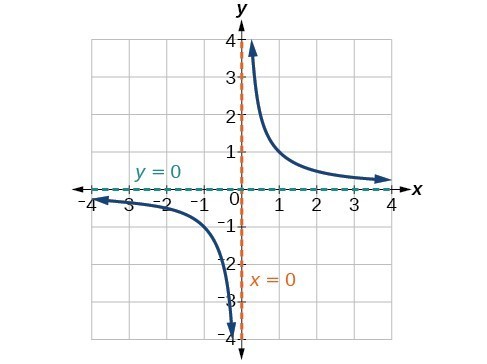



Characteristics Of Rational Functions College Algebra
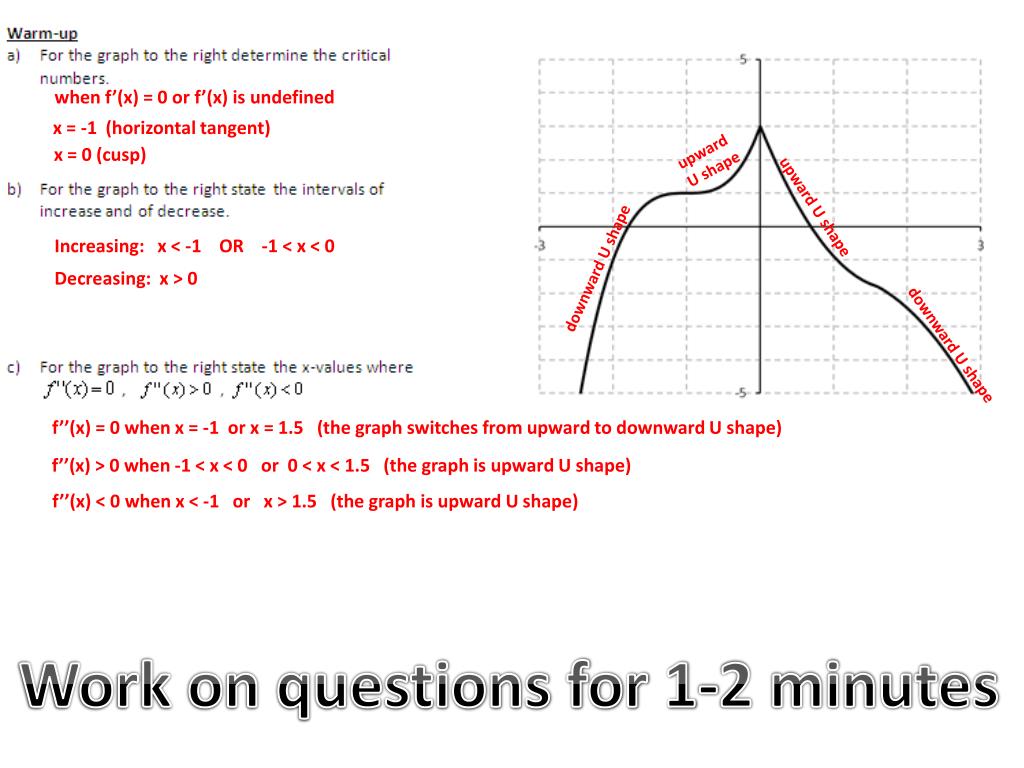



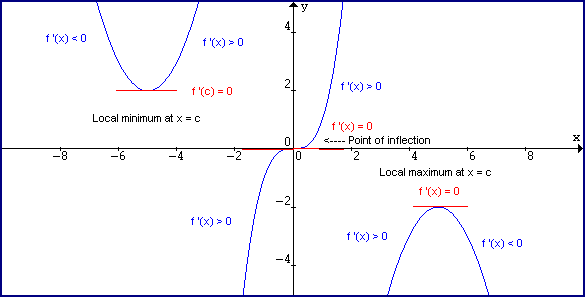
Ppt When F X 0 Or F X Is Undefined Powerpoint Presentation Id
Evaluating a Limit Using a Table of Functional Values 1 Evaluate lim x → 0 sin x x using a table of functional values Show Solution We have calculated the values of f ( x) = ( sin x) / x for the values of x listed in (Figure) Table of Functional Values for lim x → 0 sin x x xSolutionShow Solution \ \text { Given } f\left ( x \right) = x^3 6 x^2 9x\ \ \Rightarrow f'\left ( x \right) = 3 x^2 12x 9\ \ \text { For a local maxima or a local minima, we must have }\ \ f'\left ( x \right) = 0\ \ \Rightarrow 3 x^2 12x 9 = 0\ \ \Rightarrow x^2 4x 3 = 0\The value of your function, "f ()", when the argument, "x", equals 0 So, for example, if you are graphing the distance you travel on a given trip, with x representing time from the start, and f (x) representing your distance from home, you would likely start the graph at the origin, (0,0) f (0) =0 at the start of the trip




Connecting F F And F Graphically Video Khan Academy



Graphing A Function Using The First Derivative Graph Math100 Mirka
F ( 3) = 1 – ( 3) = 4 f (2) = 1 – ( 2) = 3 f ( 1) = 1 – ( 1) = 2 etc Also, f (x) = 1 for x = 0 Lastly, f ( x) = x 1 for, x > 0 and f (1) = 2, f (2) = 3, f (3) = 4, f (4) = 5 and so on Thus, the graph of f is as shown below Concept Some Functions and Their Graphs Report ErrorThis is asking me for all the values of (g o f)(x) = g(f(x)) for x = –3, –2, –1, 0, 1, 2, and 3So I'll just follow the points on the graphs and compute all the values (g o f)(–3) = g(f(–3)) = g(1) = –1I got this answer by looking at x = –3 on the f(x) graph, finding the corresponding yvalue of 1 on the f(x) graph, and using this answer as my new xvalue on the g(x) graphDefn f is concave down if the graph of f lies below the tangent lines to f Defn f is concave up if the graph of f lies above the tangent lines to f Concavity Test If f′′(x) > 0 for all x ∈(a,b), then f is concave upward on (a,b) If f′′(x) < 0 for all x ∈(a,b), then f is concave down on (a,b) Defn The point (x0,y0) is an inflection point if f is continuous at x0 and if the concavity changes at x0



Graph Of A Function Wikipedia



Business Calculus
Free functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystepSolutions to Graphing Using the First and Second Derivatives SOLUTION 1 The domain of f is all x values Now determine a sign chart for the first derivative, f ' f ' ( x) = 3 x2 6 x = 3 x ( x 2) = 0 for x =0 and x =2 See the adjoining sign chart for the first derivative, f ' Now determine a sign chart for the second derivativeGraph f(x) = −2x 2 3x – 3 a = −2, so the graph will open down and be thinner than f(x) = x 2 c = −3, so it will move to intercept the yaxis at (0, −3) Before making a table of values, look at the values of a and c to get a general idea of what the graph should look like



3



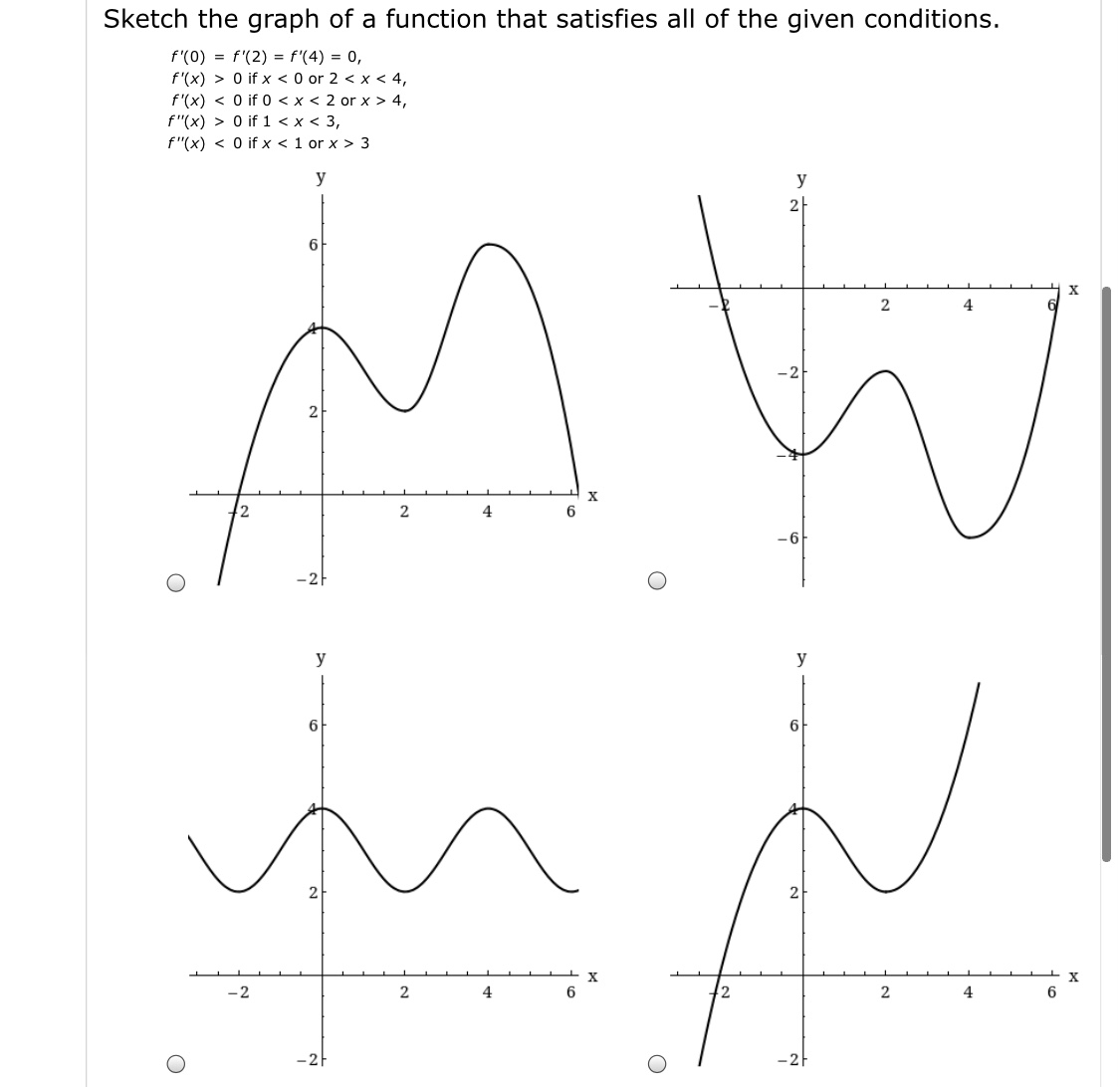
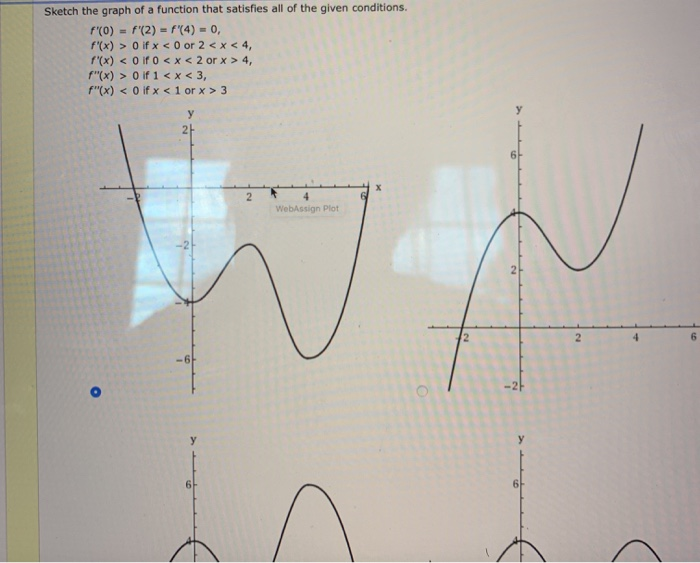
Solved Sketch The Graph Of Function F That Satisfies The Following Conditions Course Hero
The range of f is given by the interval (∞ , 1 Example 4 Find the domain of function f given below, graph it and find its range f( x ) = √ ( x 2 4) Solution to Example 4 The domain of function given above is found by solving the polynomial inequality x 2 4 ≥ 0 The solution set of the above inequality is given by the interval 2 , 2 which is also the domain of the above functionThe graph of y = f(x c) is obtained by translating the graph of y = f(x) c units to the left;Graph the linear function f given by f (x) = 2 x 4 Solution to Example 1 You need only two points to graph a linear function These points may be chosen as the x and y intercepts of the graph for example Determine the x intercept, set f (x) = 0 and solve for x 2 x 4 = 0 x = 2 Determine the y intercept, set x = 0 to find f (0)




2 Draw The Graph Of A Function With The Following Characteristics P 217 Es A F 2 F 0 L F Homeworklib



What Is The Meaning Of Math F X 0 Math And Math F X 0 Math Quora
X is not equal to 0 or 1F(x) = (c) Use calculus to find the exact maximum value of f(x) f(x) = (d) Use a graph of f '' to estimate the xcoordinates of the inflection points (Round yourThen the graph of y = f(x c) is obtained by translating the graph of y = f(x) c units to the right;
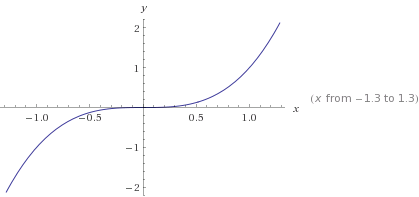



Do Local Extrema Occur If And Only If F X 0 Brilliant Math Science Wiki



Www Shsu Edu Kws006 Precalculus 1 2 Function Graphs Files S 26z 1 6 Pdf
A necessary but not sufficient condition For a function f, if its second derivative f″(x) exists at x 0 and x 0 is an inflection point for f, then f″(x 0) = 0, but this condition is not sufficient for having a point of inflection, even if derivatives of any order exist In this case, one also needs the lowestorder (above the second) nonzero derivative to be of odd order (third, fifthSelect the correct choice below and, if necessary, fill in the answer box to complete your choice OA For this equation, The parabola opens upward because a > 0, resulting in a vertex that is a minimum The yintercept of the quadratic function f (x) = x² 3x 4 is (0, c), ie, the point From we get the xintercepts at The axis of symmetry



Solution Graph The Piecewise Function Show All Work F X X If X Amp 04 0 And 0 If 0 Lt X Lt 5 And 2x 10 If X Amp 05 5 State Whether The Function Is Continuous If It Is




Extrema Of A Function
The function f(x) = x 2/3 is defined for all x and differentiable for x ≠ 0, with the derivative f ′(x) = 2x −1/3 /3 Since f is not differentiable at x=0 and f'(x)≠0 otherwise, it is the unique critical point The graph of the function f has a cusp at this point with vertical tangent The corresponding critical value is f(0) = 0We draw the graphs of f(x) = x 2 − 2x − 3 and g(x) = 2x − 3 by making a table of values and plotting the points We can see, both from the graph and from the table of values, that the graphs intersect when x = 0 and x = 4 Solving algebraically x 2 − 2x − 3 = 2x − 3 x 2 − 4x = 0 x(x − 4) = 0 Giving the solutions x = 0 and x = 42) Sketch the graph of a function whose first and second derivatives are always negative 3)



Http Hcgreen Weebly Com Uploads 4 4 3 1 Chapter 5 Review Key Pdf



Activation Functions Fundamentals Of Deep Learning
So, (1) Any line with positive slope through (2,1) meets the condition for example f (x) = 3(x − 2) 1 has f '(x) = 3 > 0 for all x ≠ 2 and also for x = 2 graph {y1=3 (x2) 1907, 919, 245, 31} Replace 3 with any positive number for another exampleF (x) < 0 if 2 < x< 0 or x > 4 2) Answer f (x) > 0 if x > 2 f (x) < 0 if x < 2 ;
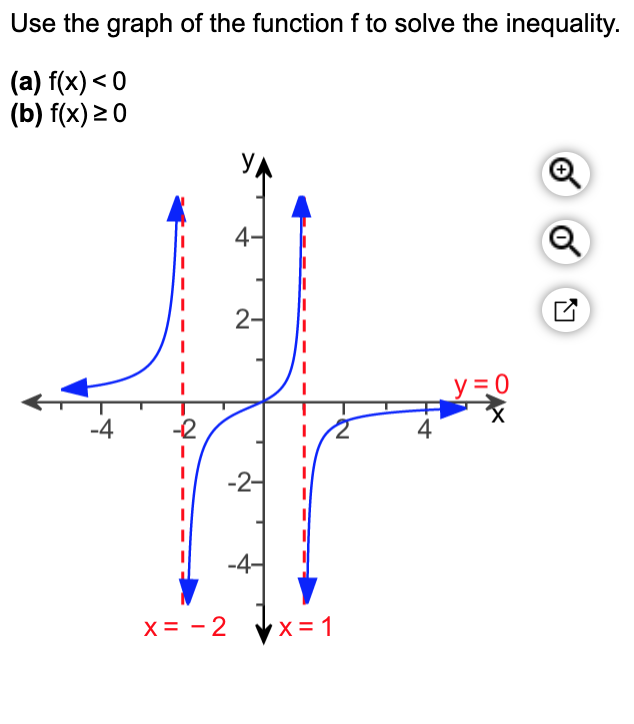



Answered Use The Graph Of The Function F To Bartleby




Graphs Of F X F X F X And X 0 F T Dt For Example 29 5 Download Scientific Diagram
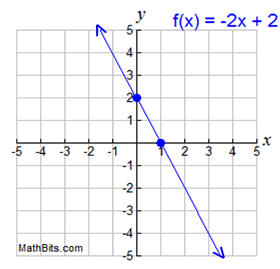



Features Of Function Graphs Mathbitsnotebook A1 Ccss Math



Graphing A Function Using The First Derivative Graph Math100 Mirka
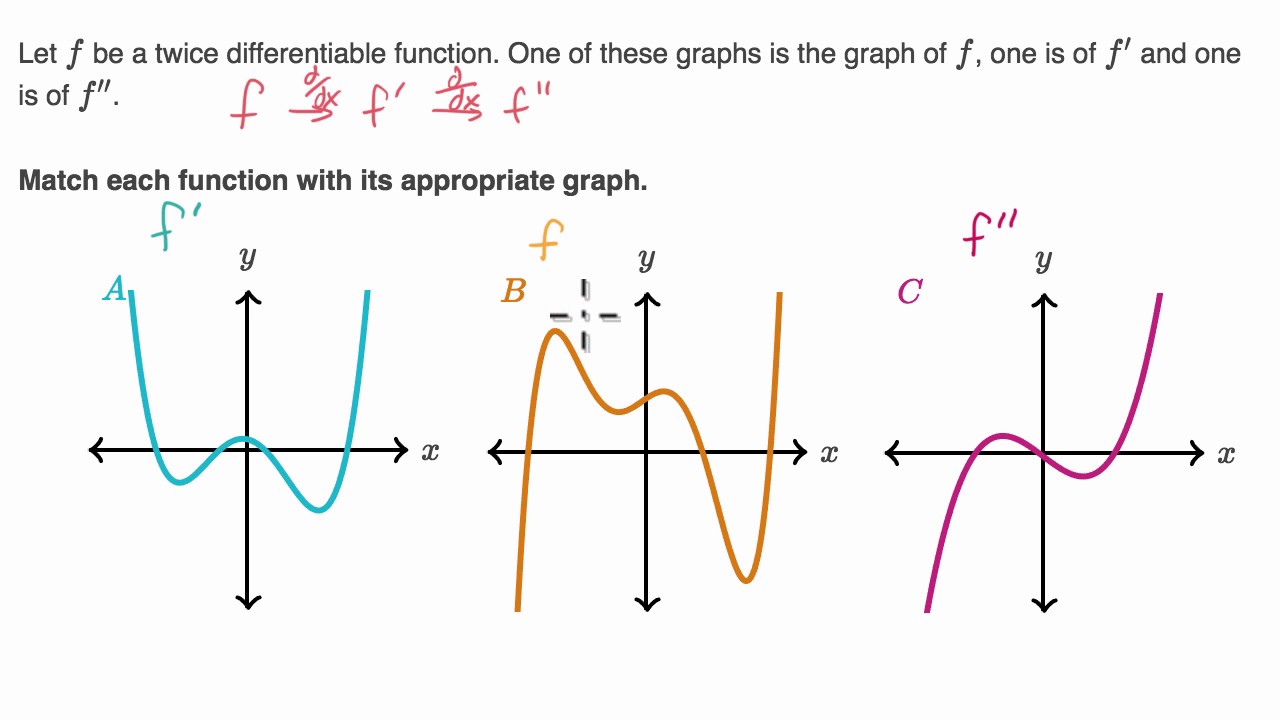



Identifying F F And F Based On Graphs Youtube




Taylor Series Wikipedia




The Graph Of F X Is Given In The Figure Below Draw The Lines To The Graph At X 4 X 3 X 0 And X 3 Estimate F 4 F 3 F 0 And F 3 Study Com




What Is The Graph Of F X To Find The Solutions To The Equation F X 0 Brainly Com



What Does F 0 Represent On The Graph Of F X Quora



Http Www Fen Bilkent Edu Tr Otekman Math101 F19 M2q1 Pdf
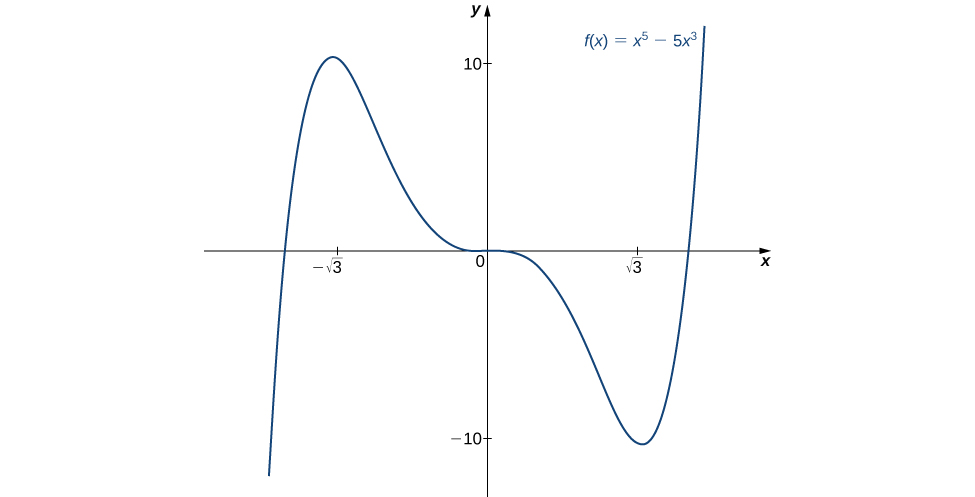



4 5 Derivatives And The Shape Of A Graph Calculus Volume 1



People Qatar Tamu Edu Tingwen Huang Math151 Fall16 5 1 Pdf
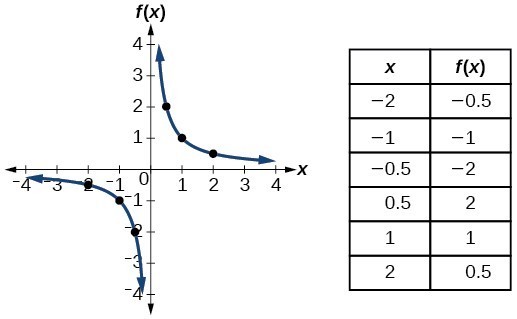



Identify Functions Using Graphs College Algebra




4 3 Connecting F And F With The Graph Of F Magic Light Calculus



Applications Of Differentiation The Graph Of A Function And Its Derivatives Extreme Points Of A Function Local Or Relative Maximum And Local Minimum Of A Function The First Derivative Test The Second




Connecting F F And F Graphically Video Khan Academy



Derivative And Tangent Line



Solving Polynomial Inequalities By Graphing



Q Tbn And9gcqythemqhzdi4g S 004oq9wf5wp F04rkzyu6vfnmlezt6voz Usqp Cau
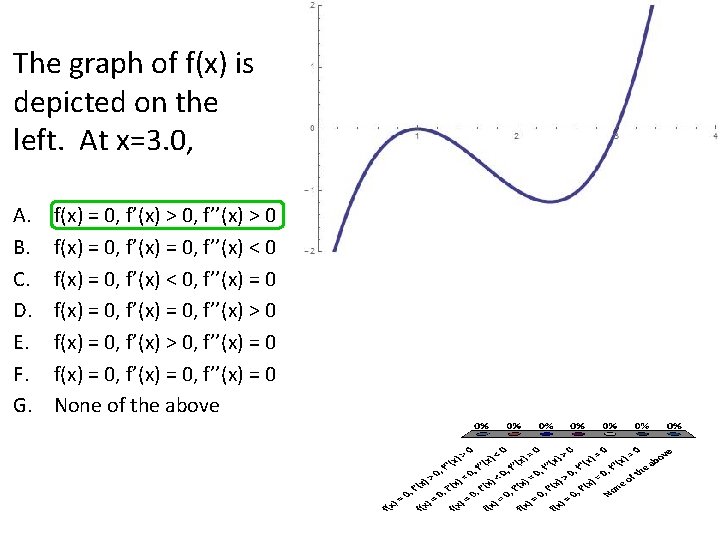



The Graph Of Fx Is Depicted On The
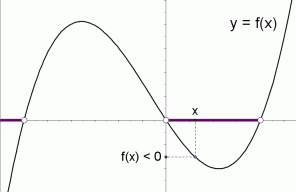



Graphical Interpretation Of Sentences Like F X 0 And F X 0
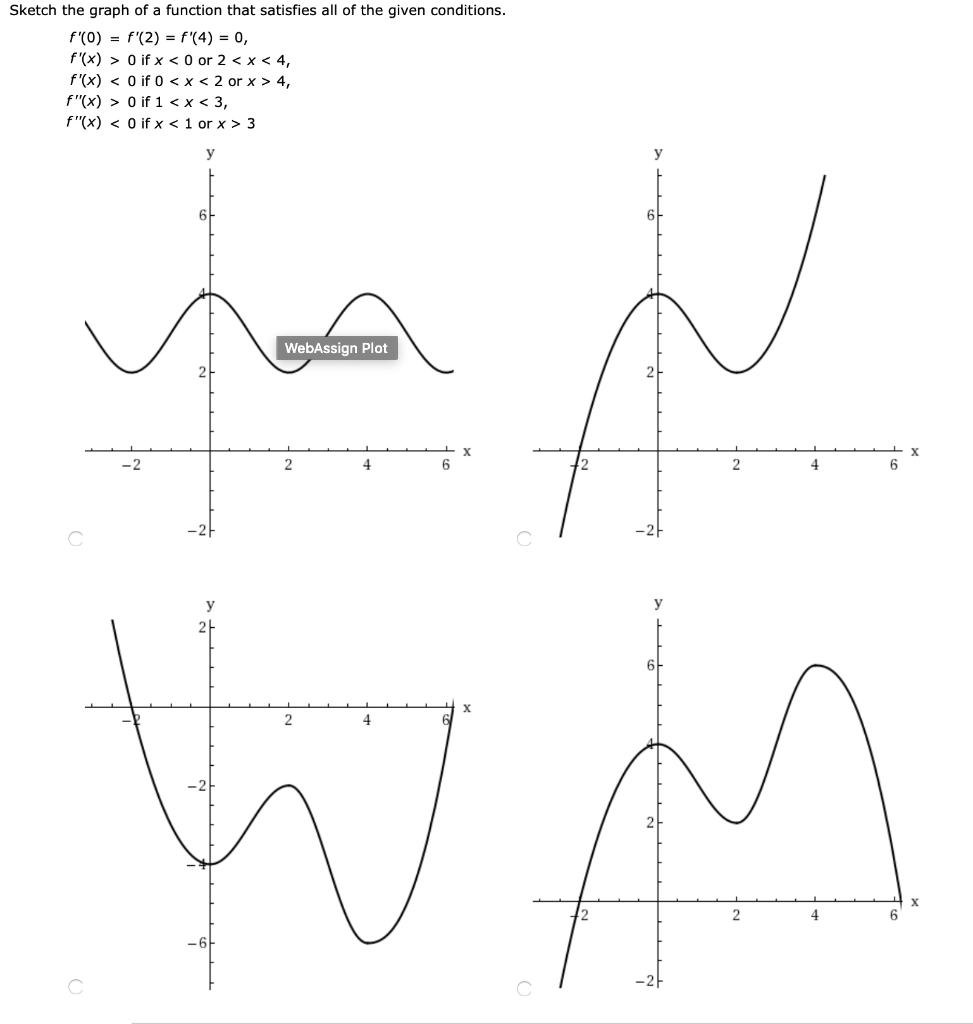



Sketch The Graph Of A Function That Satisfies All Of Chegg Com
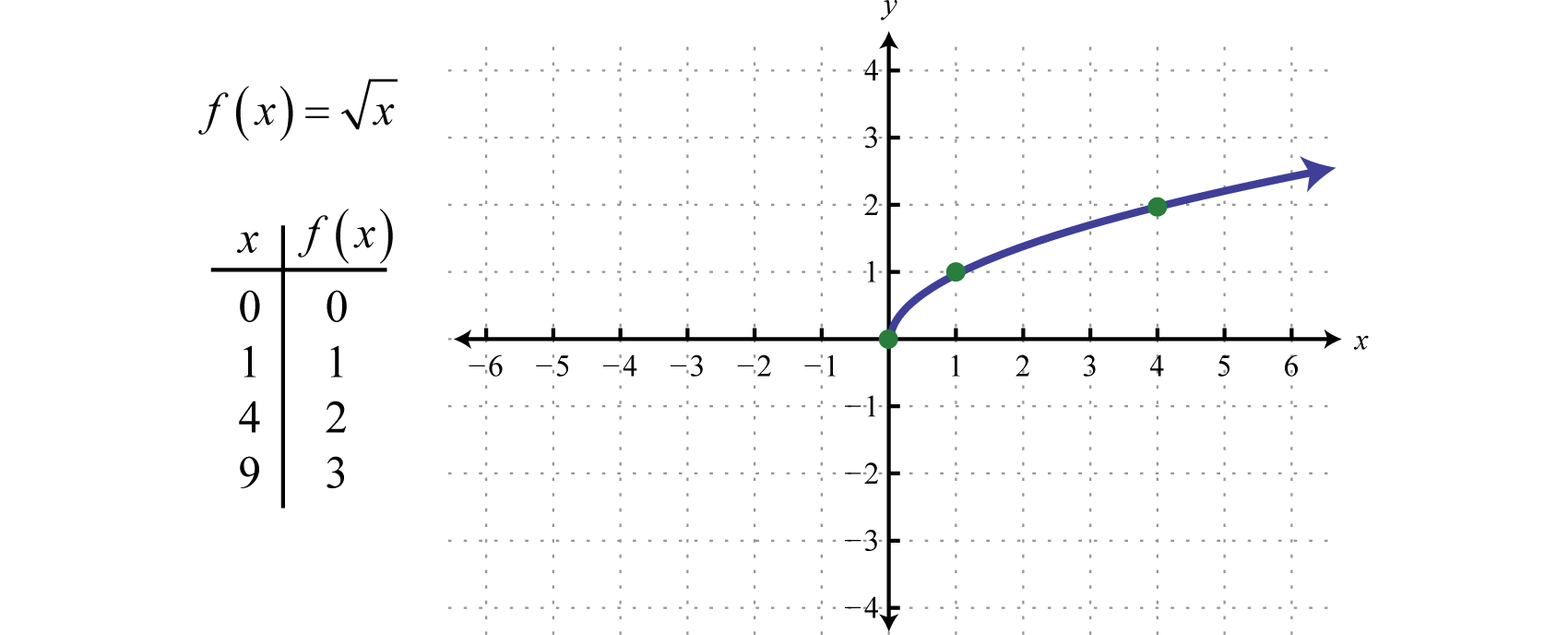



Graphing The Basic Functions



Www Freeport K12 Pa Us Userfiles 8 Classes 5535 Day 67 68 hw Pdf Id 5968




Example 22 Function F Is Defined By F X 1 X 1 X 1



Graph Of Quadratic Function



Graphical Interpretation Of Sentences Like F X 0 And F X 0



Solved Sketch The Graph Of A Function That Satisfies All Of The Following Conditions Course Hero



Answered Sketch The Graph Of A Function That Bartleby



Introduction To Exponential Functions




Piecewise Functions




Ex Determine The Sign Of F X F X And F X Given A Point On A Graph Youtube




Introduction To Functions
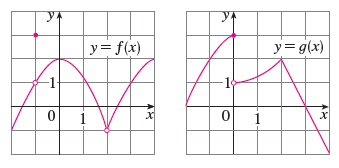



Lim X 2 F X G X B Lim X 0 F X G X C Lim X 1 F X G X D Lim X 3 F X G X E Lim X 2 X2f X F F 1 Lim X 1 G X Wyzant
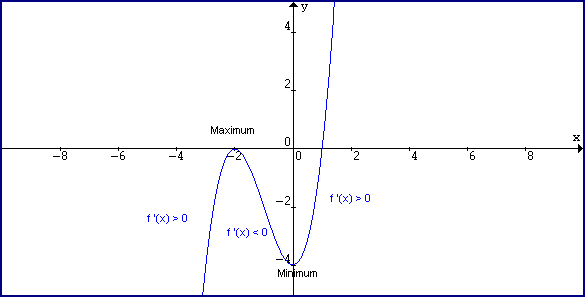



Derivative And Tangent Line



Calc 1 F X 0 If X 0 What Does This Mean Physics Forums



Sketch The Graph Of A Function That Satisfies All Of Chegg Com
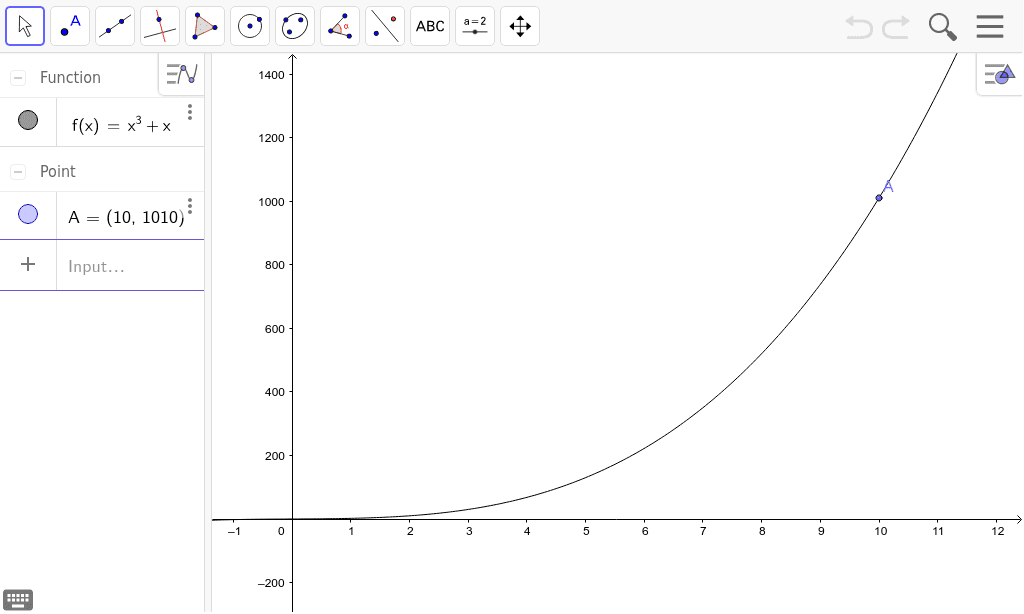



Graph Of F X X 3 X 0 X 10 Geogebra
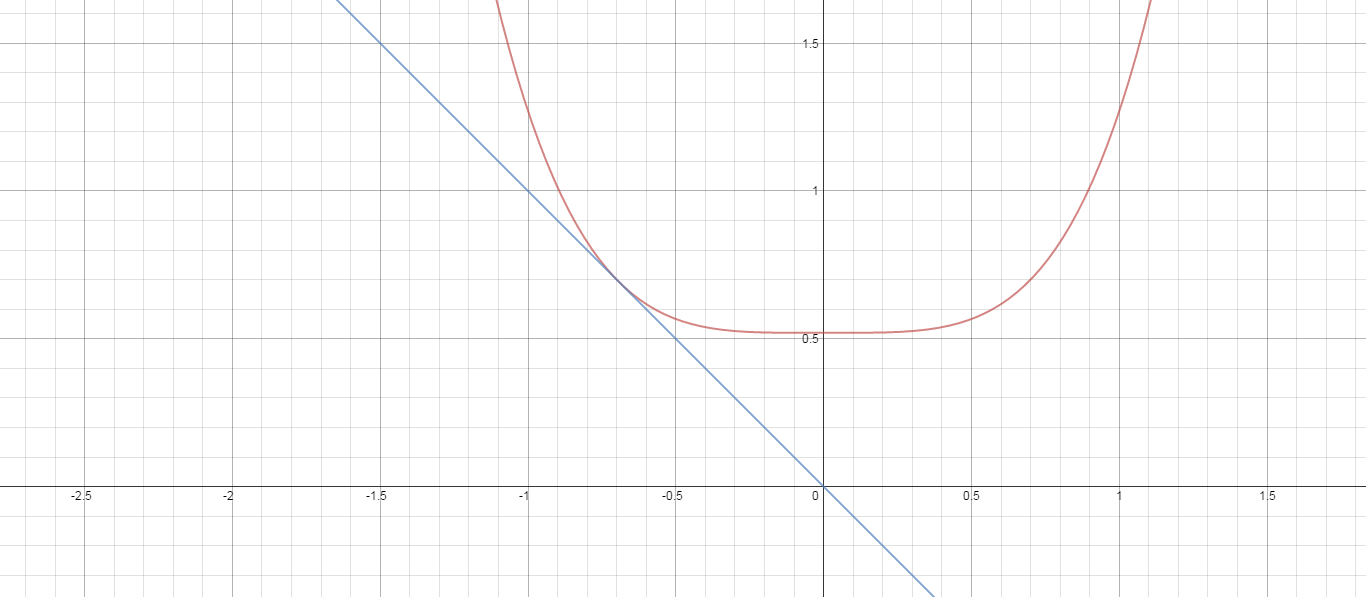



How To Find A Function F Such That F X 3x 3 And The Line X Y 0 Is Tangent To The Graph Of F Socratic




How To Use Graph To Determine Where F X 0 And F X 0 Mathematics Stack Exchange
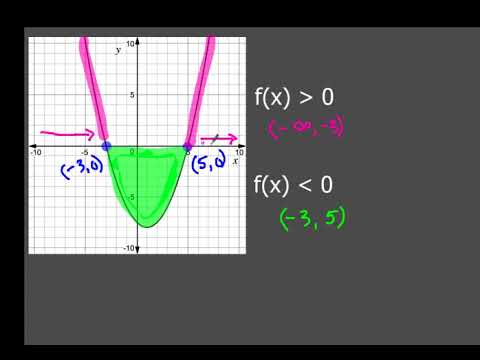



How To Tell Where F X Is Less Than 0 Or Greater Than 0 Youtube
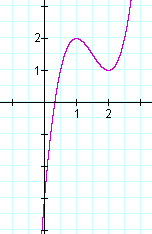



Maximum And Minimum Values An Approach To Calculus
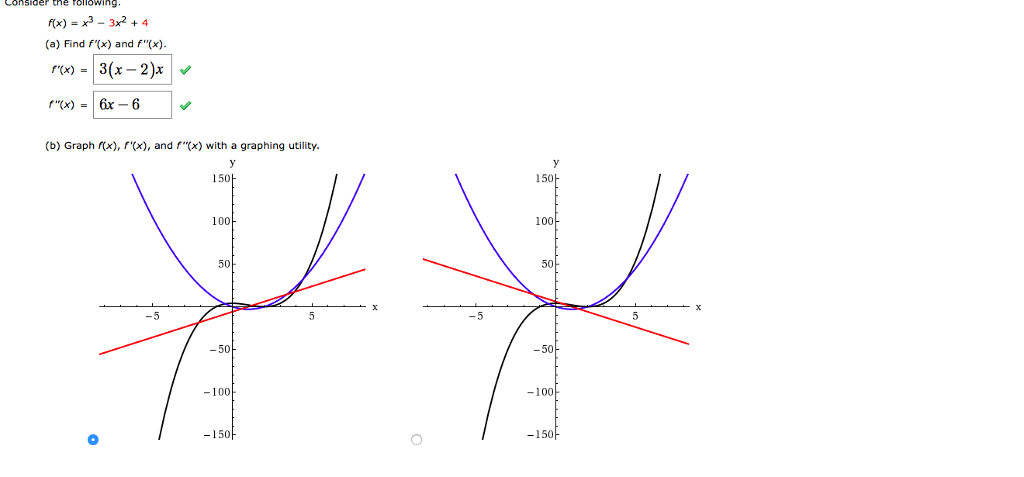



C Identify X Values Where F X 0 Enter Your Chegg Com




Need Answer Asap The Function F X Is Shown On The Graph If F X 0 What Is X Brainly Com



Math Ou Edu Forester 1914f14 Hw8 Pdf



Solving Polynomial Inequalities By Graphing




Sketch The Graph Of The Function F Given By F X X X X



Webpages Uncc Edu Sjbirdso Calc i Spr11 Hw Hw 22 Key Pdf
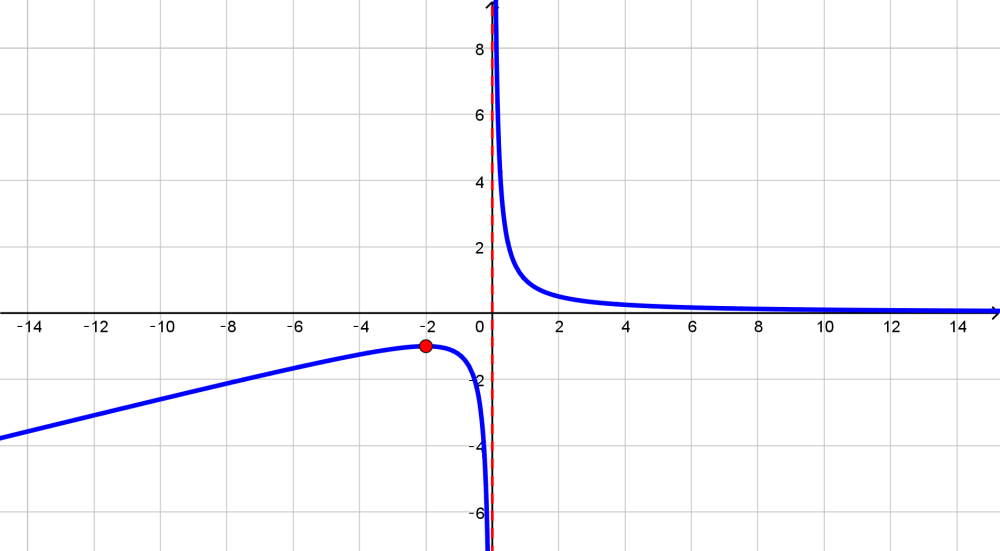



Sketch The Graph Of A Function That Satisfies All Of The Giv Quizlet
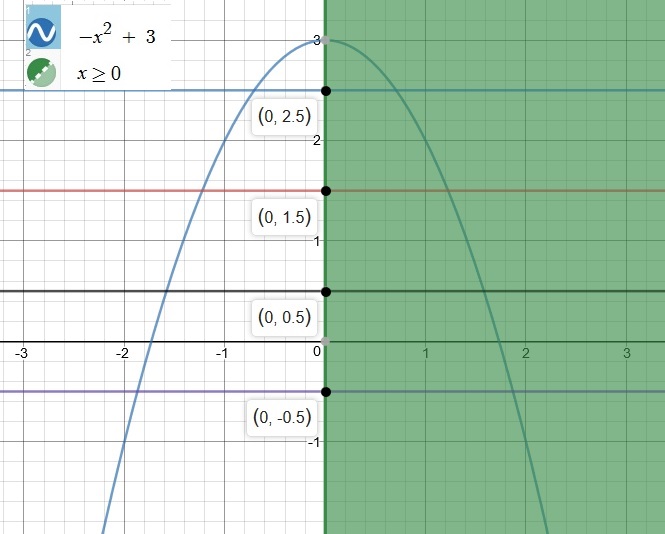



How Do You Graph F X X 2 3 X 0 And Then Use The Horizontal Test To Determine Whether The Inverse Of F Is A Function Socratic
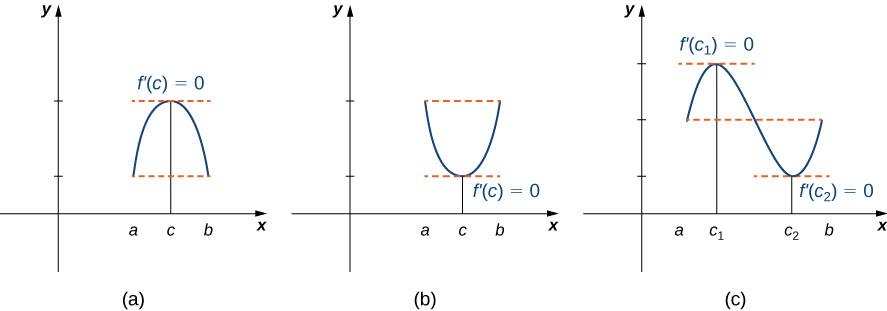



4 2 The Mean Value Theorem Mathematics Libretexts
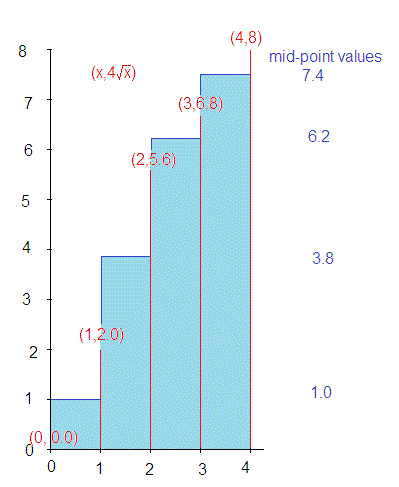



How Do You Estimate The Area Under The Graph Of F X 4sqrt X From X 0 To X 4 Using Four Approximating Rectangles And Right Endpoints Socratic
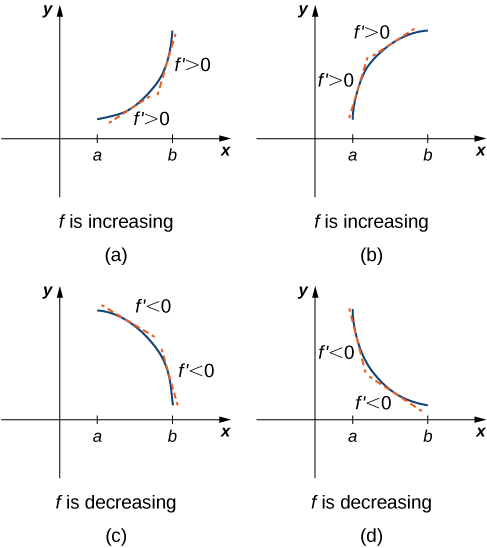



4 5 Derivatives And The Shape Of A Graph Mathematics Libretexts



Math Usu Edu Rheal Math1210 Lecture Notes Review For Midterm 2 Concepts Pdf
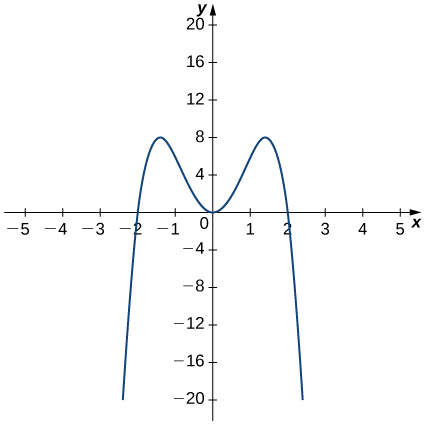



3 2 The Derivative As A Function Calculus Volume 1
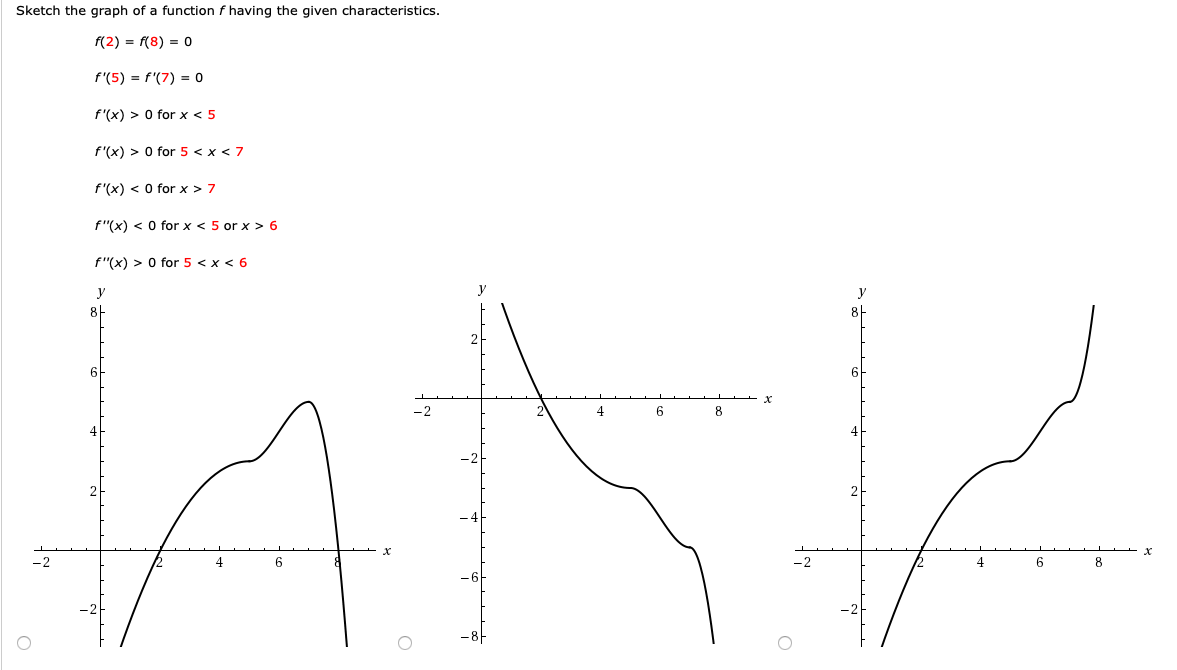



Sketch The Graph Of A Function F Having The Given Chegg Com



From The Graph Shown Find A F 1 B F 0 C 3f 2 D The Value Of X That Corresponds To F X 0 Math Homework Answers



Www Hoodriver K12 Or Us Cms Lib Or Centricity Domain 230 Ch 5 pt answer key Pdf




Analyzing Graphs Flashcards Quizlet




Match The Conditions F X Less Than 0 And F X Less Than 0 With One Of The Graphs In The Figure Study Com




I Can Sketch The Graph Of F Given The Graph Of F Ppt Download



Which One Of The Following Graph Represents The Function F X X X X 0 Sarthaks Econnect Largest Online Education Community
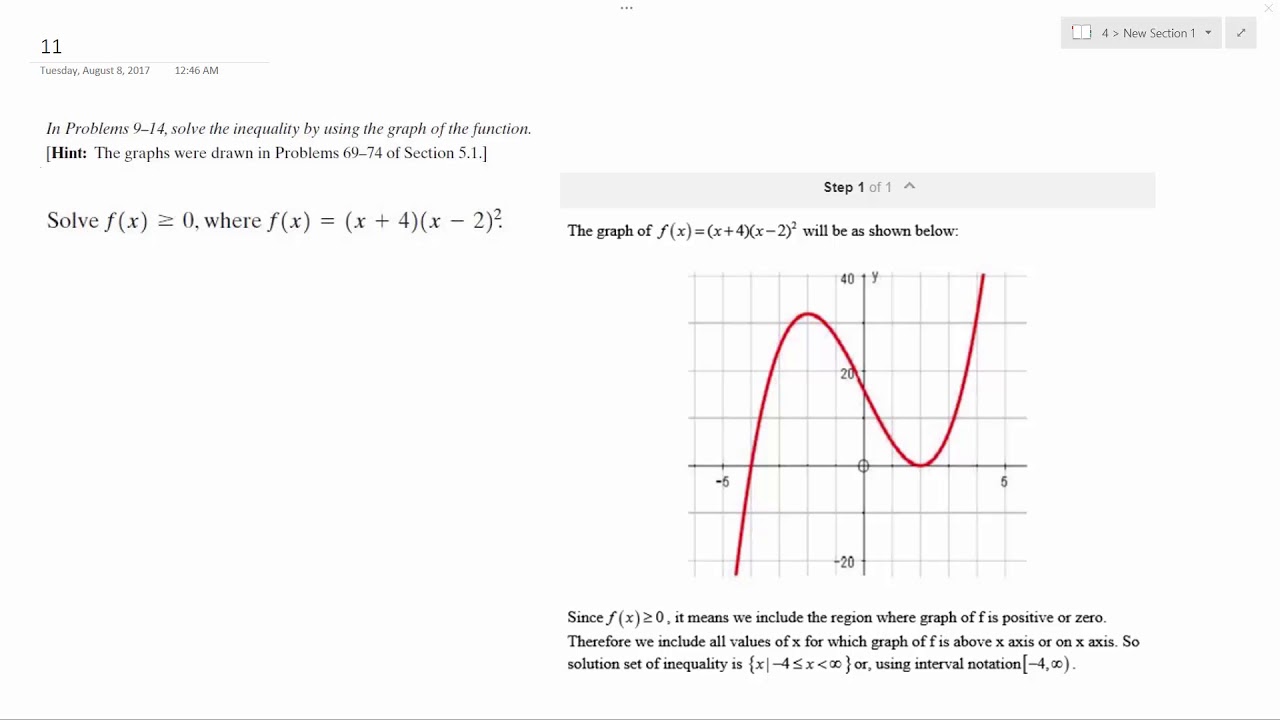



Solve F X Greater Than 0 Where F X X 4 X 2 2 Youtube



Solution Draw The Graph Of Function F X X If X Less Than Or Equal To 0 X Lt 0 X If O Less Than X Less Than Or Equal To 2 0 Lt X Lt 2 X If X Gt 2



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q5 Pdf



Search Q F F F Graphs Tbm Isch



Search Q Point Of Inflection Tbm Isch
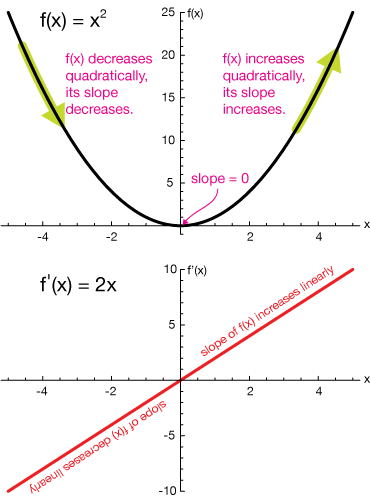



The Derivative




Use The Given Graph Of F X To Determine The Intervals Where F X Greater Than 0 F X Less Than 0 The X Values Where F X 0 And Where F X Is




The Graph Of The Function F X Is Shown Below Use The Letters Shown On The Graph To Answer The Following Questions A Find The Value S Of X Where F X 0 B




The Graph Of F Is Locally Linear At X 0 As Is Suggested By Zooming In Download Scientific Diagram



Http Smacmathapcalculus Weebly Com Uploads 1 9 2 5 Apc Hw 4 6 Key Pdf




Each Of The Following Graphs Represent Y F X Find The Indicated Value For Each Of The Following From The Graph Mathematics Stack Exchange
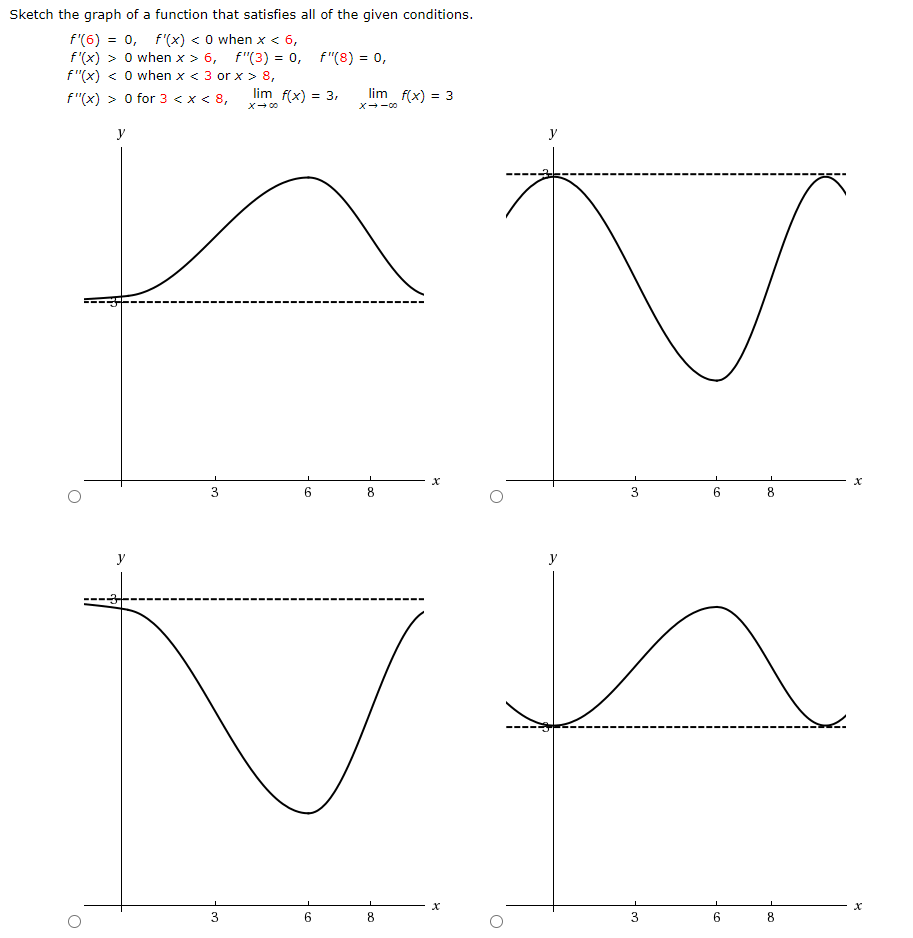



Sketch The Graph Of A Function That Satisfies All Of Chegg Com



0 件のコメント:
コメントを投稿